Case-Study zur Arbeitslosigkeit in Deutschland

Organisatorische Hinweise

Bitte bis zum 09.05.2021 angeben ob Sie bei den Projekten in Gruppen zugeteilt werden dürfen
- Ohne Zusage keine Gruppe
- Ohne Gruppe keine Note
Am 10.05.2021 erfolgt die Zuteilung auf Gruppen und die Tutoriumstermine werden freigegeben

Weitere Daten:

Bis zum 09.05.2021 ist das 5. R-Tutor Problem Set auf Moodle hochzuladen (nur die .sub-Datei!)
Bis zum 16.05.2021 ist das 6. R-Tutor Problem Set auf Moodle hochzuladen (nur die .sub-Datei!)
Ab dem 17.05.2021 steht für Sie wieder eine Probeklausur auf Moodle bereit

Recap der VorlesungsinhalteWir hatten die Wahrscheinlichkeitstheorie und die Normalverteilung besprochen
Wir hatten über die Stichprobenvarianz, Standardfehler und Konfidenzintervalle gesprochen
Wir hatten einen Hypothestest durchgeführt
Wir hatten die Korrelation von zwei Variablen und die lineare Regression betrachtet
Anschließend sind wir in der multiplen linearen Regression auch auf Interaktionsterme eingegangen

Empirische Analyse unserer Case-Study

Induktive StatistikInteresse gilt nicht dem Datensatz selbst, sondern der PopulationSie haben keine Vollerhebung durchgeführt, sondern nur eine (zufällige) Stichprobe der Population gezogen

Beispiel: Mikrozensus, d.h. eine Befragung von zufällig ausgewählten Haushalten in Deutschland
Sie wollen aus der Stichprobe schätzen, wie sich die beobachtete Größe in der Population verhält
Es gibt viele Arten der induktiven Statistik. Die zwei häufigsten:Vorhersage
Erkennen kausaler Zusammenhänge

Bereiche der induktiven StatistikStichprobentheorieGüte der Stichprobe; Wichtig um repräsentative Ergebnisse zu erhalten

SchätztheoriePunktschätzer und Konfidenzintervalle

TesttheorieHypothesentest, lineare Regression

Wie sieht die induktive Statistik in der Praxis aus?

Dritter Teil der Case Study

Daten aus der Case-Study, welche wir im vorherigen Semester eingelesen und deskriptiv analysiert haben wollen wir nun mittels der induktiven Statistik näher untersuchen.

Erster Schritt: Kurzer Recap mittels bivariater deskriptiver Statistik um den Zusammenhang verschiedener Variablen darzustellen
Zweiter Schritt: (Multiple) lineare Regression der Daten um herauszufinden, welche Faktoren die Arbeitslosenquote in den deutschen Landkreisen treibt
- Darstellung mit dem Paket stargazer

Dritter Teil der Case Study

Daten aus der Case-Study, welche wir im vorherigen Semester eingelesen und deskriptiv analysiert haben wollen wir nun mittels der induktiven Statistik näher untersuchen.

Erster Schritt: Kurzer Recap mittels bivariater deskriptiver Statistik um den Zusammenhang verschiedener Variablen darzustellen
Zweiter Schritt: (Multiple) lineare Regression der Daten um herauszufinden, welche Faktoren die Arbeitslosenquote in den deutschen Landkreisen treibt
- Darstellung mit dem Paket stargazer

Ziele des dritten Teils der Case Study:

(Multiple) lineare Regression und Interpretation der Koeffizienten
Interaktionsterme
Besprechen der Kausalität

Dritter Teil der Case Study

Daten aus der Case-Study, welche wir im vorherigen Semester eingelesen und deskriptiv analysiert haben wollen wir nun mittels der induktiven Statistik näher untersuchen.

Erster Schritt: Kurzer Recap mittels bivariater deskriptiver Statistik um den Zusammenhang verschiedener Variablen darzustellen
Zweiter Schritt: (Multiple) lineare Regression der Daten um herauszufinden, welche Faktoren die Arbeitslosenquote in den deutschen Landkreisen treibt
- Darstellung mit dem Paket stargazer

Ziele des dritten Teils der Case Study:

(Multiple) lineare Regression und Interpretation der Koeffizienten
Interaktionsterme
Besprechen der Kausalität

Im vierten RTutor Problem Set beschäftigen Sie sich auch mit der linearen Regression zu einzelnen Ländern auf europäischer Ebene und im 5. und 6. Problem Set geht es um die Kausalität.

Daten und Pakete laden

Wir laden die aus Teil 1 der Case-Study erstellten Datensätze:

library(tidyverse)
library(stargazer)
library(corrr)

# Daten einlesen
bip_zeitreihe <- readRDS("../case-study/data/bip_zeitreihe.rds")
gesamtdaten <- readRDS("../case-study/data/gesamtdaten.rds")
# Zuerst wollen wir die Arbeitslosenquote, einen Dummy für Ostdeutschland und die Verschuldung im Verhältnis zum BIP pro Landkreisberechnen
gesamtdaten <- gesamtdaten %>%
  mutate(alo_quote = (total_alo / (erw+total_alo))*100,
         ost = as.factor(ifelse(bundesland_name %in% c("Brandenburg", "Mecklenburg-Vorpommern", "Sachsen", "Sachsen-Anhalt", "Thüringen"), 1, 0)),
         ost_name = ifelse(ost == 1, "Ostdeutschland", "Westdeutschland"),
         anteil_schulden = (Schulden_gesamt / bip)*100)
bip_wachstum <- bip_zeitreihe %>%
  filter( nchar(Regionalschluessel) == 5) %>%
  group_by(Regionalschluessel) %>%
  arrange(Jahr) %>%
  mutate( bip_wachstum = 100*(bip - lag(bip)) / bip ) %>%
  ungroup() %>%
  filter( Jahr == 2017 ) %>%
  select(Regionalschluessel, bip_wachstum, Jahr)
gesamtdaten <- left_join(gesamtdaten, bip_wachstum, by = "Regionalschluessel")

Bivariate deskriptive Analysen (Korrelationen)

Korrelation zwischen den einzelnen Variablen

Wir hatten uns im letzten Semester bereits die Korrelation der einzelnen Variablen angeschaut und wollen diese Korrelationen noch einmal aufgreifen:

Korrelation zwischen den einzelnen Variablen

Wir hatten uns im letzten Semester bereits die Korrelation der einzelnen Variablen angeschaut und wollen diese Korrelationen noch einmal aufgreifen:

Bevor wir uns der Regressionsanalyse zuwenden schauen wir uns den Zusammenhang der unterschiedlichen Variablen erst visuell noch einmal an.

Wie hoch ist die Korrelation zwischen Arbeitslosenquote und BIP Wachstum?
Wie hoch ist sie zwischen Arbeitslosenquote und dem Anteil der Schulden?
Und schlussendlich: Wie hoch ist die Korrelation zwischen dem BIP Wachstum und dem Anteil der Schulden?

Korrelation zwischen den einzelnen Variablen

Wir hatten uns im letzten Semester bereits die Korrelation der einzelnen Variablen angeschaut und wollen diese Korrelationen noch einmal aufgreifen:

Bevor wir uns der Regressionsanalyse zuwenden schauen wir uns den Zusammenhang der unterschiedlichen Variablen erst visuell noch einmal an.

Wie hoch ist die Korrelation zwischen Arbeitslosenquote und BIP Wachstum?
Wie hoch ist sie zwischen Arbeitslosenquote und dem Anteil der Schulden?
Und schlussendlich: Wie hoch ist die Korrelation zwischen dem BIP Wachstum und dem Anteil der Schulden?

Hierdurch bekommen wir einen ersten Eindruck der Daten und werden auf mögliche Probleme aufmerksam, wie z.B. Multikolliniarität.

Korrelation zwischen der Arbeitslosenquote und dem BIP Wachstum

cor_alo_bip <- cor(gesamtdaten$alo_quote, 
    gesamtdaten$bip_wachstum,
    use = "pairwise.complete.obs")
gesamtdaten %>%
  ggplot(aes(x = bip_wachstum, y = alo_quote)) + 
  geom_point() + 
  labs( x = "Wachstum des BIP %", 
        y = "Arbeitslosenquote in %",
        title = "Korrelation des BIP-Wachstums und der Arbeitslosenquote") +
  theme_minimal() +
  geom_text(x = 0.02, y =13, label = paste("r = ", as.character(round(cor_alo_bip,2))))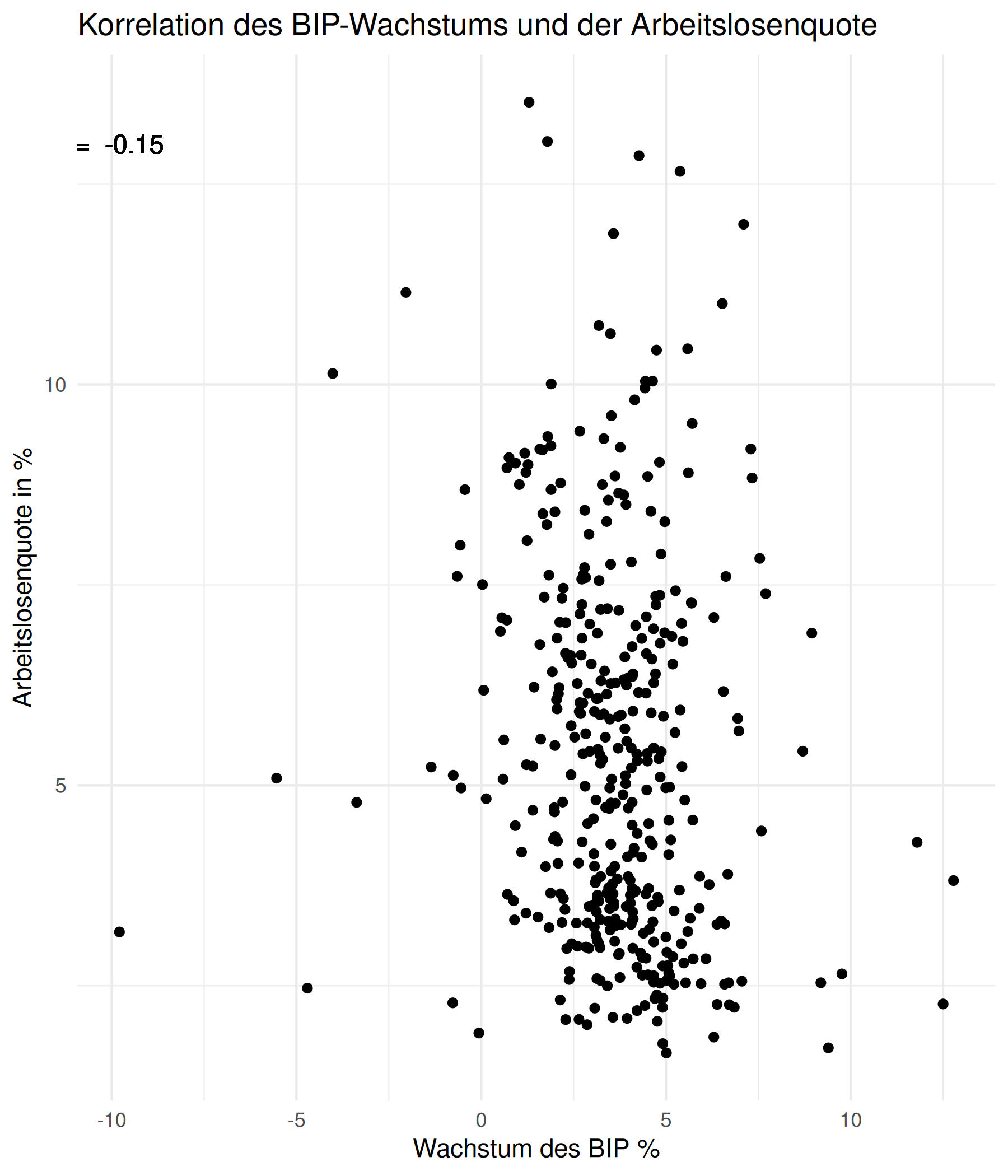

Korrelation zwischen der Arbeitslosenquote und dem Anteil der Schuldencor_alo_verschuldung <- cor(gesamtdaten$alo_quote, gesamtdaten$anteil_schulden,use = "pairwise.complete.obs")
gesamtdaten %>%
  ggplot(aes(x = anteil_schulden, y = alo_quote)) + 
  geom_point() + 
  labs( x = "Anteil der Schulden am BIP in %", 
        y = "Arbeitslosenquote in %",
        title = "Korrelation der öffentlichen Verschuldung und der Arbeitslosenquote") +
  theme_minimal() +
  geom_text(x = 0.02, y =13, label = paste("r = ", as.character(round(cor_alo_verschuldung,2))))

Korrelation zwischen der Arbeitslosenquote und dem Anteil der Schulden

cor_alo_verschuldung <- cor(gesamtdaten$alo_quote, gesamtdaten$anteil_schulden,use = "pairwise.complete.obs")
gesamtdaten %>%
  ggplot(aes(x = anteil_schulden, y = alo_quote)) + 
  geom_point() + 
  labs( x = "Anteil der Schulden am BIP in %", 
        y = "Arbeitslosenquote in %",
        title = "Korrelation der öffentlichen Verschuldung und der Arbeitslosenquote") +
  theme_minimal() +
  geom_text(x = 0.02, y =13, label = paste("r = ", as.character(round(cor_alo_verschuldung,2))))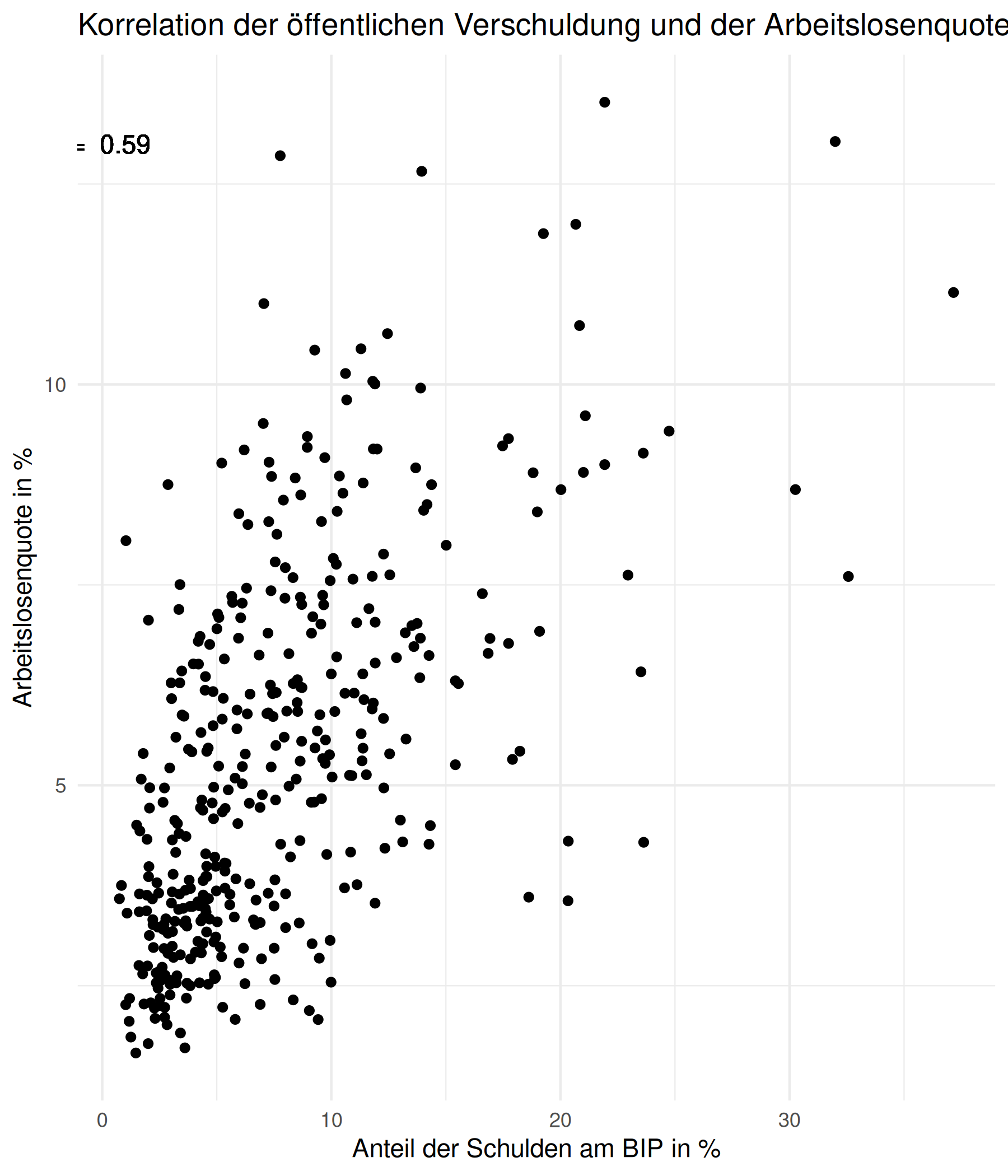

Korrelationsmatrix

korrelationen <- gesamtdaten %>%
  select(bip_wachstum, anteil_schulden, alo_quote) %>%
  correlate() %>% # Korrelationen erzeugen
  rearrange() %>%  # Sortieren nach Korrelation
  shave() # Oberen Teil der Tabelle abschneiden
fashion(korrelationen)

##           rowname bip_wachstum anteil_schulden alo_quote
## 1    bip_wachstum                                       
## 2 anteil_schulden         -.13                          
## 3       alo_quote         -.15             .59

Interpretation der KorrelationHat an sich keine intuitive quantitative Interpretation
Ist eine univariate Repräsentation des Zusammenhangs zweier Variablen
Kann dabei helfen stark korrelierte Variablen im Datensatz aufzuzeigenDies ist für eine spätere lineare Regression wichtig
Stichwort Multikollinearität

Interpretation der Korrelation

Hat an sich keine intuitive quantitative Interpretation
Ist eine univariate Repräsentation des Zusammenhangs zweier Variablen
Kann dabei helfen stark korrelierte Variablen im Datensatz aufzuzeigen
- Dies ist für eine spätere lineare Regression wichtig
- Stichwort Multikollinearität

In empirischen Arbeiten wird meist auf die lineare Regression zurückgegriffen und nicht auf die Analyse von Korrelationen:

Schätzer aus der linearen Regression sind BLUE (best linear unbiased estimator)
Wir können auf mehrere Variablen kontrollieren in der linearen Regression

Einfache lineare Regression

Lineare Regression

Zur weiteren Analyse wollen wir uns der linearen Regression bedienen:

$y_{i} = β_{0} + β_{1} x_{i} + ε_{i}, i = 1, \dots, N$

Wobei wir die Arbeitslosenquote ( $y_{i}$ ) auf das BIP Wachstum ( $x_{i}$ ) regressieren.

Arbeitslosenquote auf das BIP Wachstum regressieren

bip <- lm(alo_quote ~ bip_wachstum, data = gesamtdaten)
stargazer(bip, 
          type = "html", header = FALSE, digits = 2,
          title = "Arbeitslosigkeit auf BIP-Wachstum",
          dep.var.labels=c("Alo-quote"),
          covariate.labels="BIP-Wachstum"
          )

Arbeitslosenquote auf das BIP Wachstum regressierenArbeitslosigkeit auf BIP-Wachstum
Dependent variable:
Alo-quote
BIP-Wachstum-0.17***
(0.05)
Constant5.93***
(0.23)
Observations399
R20.02
Adjusted R20.02
Residual Std. Error2.34 (df = 397)
F Statistic9.41*** (df = 1; 397)
Note:*p<0.1; **p<0.05; ***p<0.01

**Arbeitslosigkeit auf BIP-Wachstum**

	Dependent variable:

	Alo-quote

BIP-Wachstum	-0.17^***
	(0.05)

Constant	5.93^***
	(0.23)


Observations	399
R²	0.02
Adjusted R²	0.02
Residual Std. Error	2.34 (df = 397)
F Statistic	9.41^*** (df = 1; 397)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Erkenntnisse aus der Regressionstabelle

399 Beobachtungen
R² mit 0.02 recht klein
- R² kann künstlich nach oben getrieben werden, darum besser adjusted R² anschauen
R² ist irrelevant wenn wir unsere Schätzer kausal interpetieren wollen
- R² misst die Variation in $y$ , diese wollen wir aber gar nicht erklären, sondern ob $x$ einen kausalen Einfluss auf $y$ hat!
R² ist wichtiger bei Vorhersagen
- Bei Vorhersagen möchten wir nach Möglichkeit $y$ so gut es geht erklären.
Bei Zeitreihendaten ist das R² tendenziell immer höher als bei Querschnitts- oder Paneldaten

Bitte fixieren Sie sich in ihrer Interpretation nicht auf das R²!

Erkenntnisse aus der Regressionstabelle

Interessanter: Der geschätze Koeffizient zum BIP-Wachstum in höhe von 0,17.

Wie kann dieser Koeffizient interpretiert werden?

Erkenntnisse aus der Regressionstabelle

Interessanter: Der geschätze Koeffizient zum BIP-Wachstum in höhe von 0,17.

Wie kann dieser Koeffizient interpretiert werden?

Eine um 1 Prozentpunkt höheres BIP Wachstum korrespondiert im Durchschnitt mit einer um 0,17 Prozentpunkte niedrigeren Arbeitslosenquote.

Erkenntnisse aus der Regressionstabelle

Interessanter: Der geschätze Koeffizient zum BIP-Wachstum in höhe von 0,17.

Wie kann dieser Koeffizient interpretiert werden?

Eine um 1 Prozentpunkt höheres BIP Wachstum korrespondiert im Durchschnitt mit einer um 0,17 Prozentpunkte niedrigeren Arbeitslosenquote.

Wie kann die Konstante interpretiert werden?

Erkenntnisse aus der Regressionstabelle

Interessanter: Der geschätze Koeffizient zum BIP-Wachstum in höhe von 0,17.

Wie kann dieser Koeffizient interpretiert werden?

Eine um 1 Prozentpunkt höheres BIP Wachstum korrespondiert im Durchschnitt mit einer um 0,17 Prozentpunkte niedrigeren Arbeitslosenquote.

Wie kann die Konstante interpretiert werden?

Die erwartete Arbeitslosenquote bei einem Wachstum von 0% liegt im Durchschnitt bei 5,93 Prozent.

Erkenntnisse aus der Regressionstabelle

Weitere wichtige Erkenntnis aus der Tabelle:

Der Koeffizient von BIP-Wachstum ist auf dem 1%-Niveau signifikant

Woran kann dies gesehen werden?

Erkenntnisse aus der Regressionstabelle

Weitere wichtige Erkenntnis aus der Tabelle:

Der Koeffizient von BIP-Wachstum ist auf dem 1%-Niveau signifikant

Woran kann dies gesehen werden?

Wie hoch ist die t-Statistik für unseren Koeffizienten BIP-Wachstum?

Erkenntnisse aus der Regressionstabelle

Weitere wichtige Erkenntnis aus der Tabelle:

Der Koeffizient von BIP-Wachstum ist auf dem 1%-Niveau signifikant

Woran kann dies gesehen werden?

Wie hoch ist die t-Statistik für unseren Koeffizienten BIP-Wachstum?

Landkreise mit einem höheren BIP Wachstum könnten neue Unternehmen angesiedelt haben, welche neue Mitarbeiter brauchen. Daher würde ein entsprechend negativer Zusammenhang zwischen BIP-Wachstum und Arbeitslosenquote unseren Erwartungen entsprechen.

Arbeitslosenquote auf öffentliche Schulden regressieren

schulden <- lm(alo_quote ~ anteil_schulden, data=gesamtdaten)
stargazer(schulden, 
          type = "html", header = FALSE, digits = 2,
          title = "Arbeitslosigkeit auf Anteil der Schulden pro Landkreis",
          dep.var.labels=c("Alo-quote"),
          covariate.labels="Anteil der Schulden"
          )

Arbeitslosenquote auf öffentliche Schulden regressierenArbeitslosigkeit auf Anteil der Schulden pro Landkreis
Dependent variable:
Alo-quote
Anteil der Schulden0.25***
(0.02)
Constant3.37***
(0.16)
Observations397
R20.35
Adjusted R20.35
Residual Std. Error1.90 (df = 395)
F Statistic215.18*** (df = 1; 395)
Note:*p<0.1; **p<0.05; ***p<0.01

**Arbeitslosigkeit auf Anteil der Schulden pro Landkreis**

	Dependent variable:

	Alo-quote

Anteil der Schulden	0.25^***
	(0.02)

Constant	3.37^***
	(0.16)


Observations	397
R²	0.35
Adjusted R²	0.35
Residual Std. Error	1.90 (df = 395)
F Statistic	215.18^*** (df = 1; 395)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Erkenntnisse aus der Regressionstabelle

Der geschätze Koeffizient zum Anteil der öffentlichen Schulden lieg bei 0,25.

Wie kann dieser Koeffizient interpretiert werden?

Erkenntnisse aus der Regressionstabelle

Der geschätze Koeffizient zum Anteil der öffentlichen Schulden lieg bei 0,25.

Wie kann dieser Koeffizient interpretiert werden?

Eine um 1 Prozentpunkt höhere Verschuldung korrespondiert im Durchschnitt mit einer um 0,25 Prozentpunkte höheren Arbeitslosenquote

Erkenntnisse aus der Regressionstabelle

Der geschätze Koeffizient zum Anteil der öffentlichen Schulden lieg bei 0,25.

Wie kann dieser Koeffizient interpretiert werden?

Eine um 1 Prozentpunkt höhere Verschuldung korrespondiert im Durchschnitt mit einer um 0,25 Prozentpunkte höheren Arbeitslosenquote

Die Interpretation der Konstante wäre dann wie folgt:

Für einen Landkreis ohne Verschuldung wäre die erwartete Arbeitslosenquote im Durchschnitt bei 3,37 Prozent.

Erkenntnisse aus der Regressionstabelle

Der geschätze Koeffizient zum Anteil der öffentlichen Schulden lieg bei 0,25.

Wie kann dieser Koeffizient interpretiert werden?

Eine um 1 Prozentpunkt höhere Verschuldung korrespondiert im Durchschnitt mit einer um 0,25 Prozentpunkte höheren Arbeitslosenquote

Die Interpretation der Konstante wäre dann wie folgt:

Für einen Landkreis ohne Verschuldung wäre die erwartete Arbeitslosenquote im Durchschnitt bei 3,37 Prozent.

Ein stark verschuldeter öffentlicher Haushalt hat potentiell weniger Gewerbeeinnahmen und da dort potentiell weniger Unternehmen vorhanden sind in denen Arbeitnehmer angestellt sein könnten.

Multiple lineare Regression

Sowohl das BIP Wachstum, als auch die öffentliche Verschuldung sind wichtige Faktoren zur Erklärung der Arbeitslosenquote
Öffentliche Verschuldung schien wichtiger zu sein, doch können wir beide Variablen in EINE Regression aufnehmen?

$y_{i} = β_{0} + β_{1} x_{i 1} + β_{2} x_{i 2} + . . . + β_{K} x_{i K} + ε_{i}, i = 1, \dots, N$

Durch die multiple lineare Regression können wir den Effekt einer unabhängigen Variablen auf die abhängige Variable untersuchen und zusätzlich auf den Effekt anderer Variablen kontrollieren.
Konkret: BIP-Wachstum und öffentliche Verschuldung in eine Regression packen!

Multiple lineare Regression

multi <- lm(alo_quote ~ anteil_schulden + bip_wachstum, data=gesamtdaten)
stargazer(multi,
          type = "html", header = FALSE, digits = 2,
          title = "Arbeitslosigkeit auf Anteil Schulden und BIP-Wachstum",
          dep.var.labels=c("Alo-quote"),
          covariate.labels=c("Anteil der Schulden", "BIP-Wachstum")
          )

Multiple lineare RegressionArbeitslosigkeit auf Anteil Schulden und BIP-Wachstum
Dependent variable:
Alo-quote
Anteil der Schulden0.25***
(0.02)
BIP-Wachstum-0.09*
(0.04)
Constant3.71***
(0.24)
Observations397
R20.36
Adjusted R20.36
Residual Std. Error1.89 (df = 394)
F Statistic110.18*** (df = 2; 394)
Note:*p<0.1; **p<0.05; ***p<0.01

**Arbeitslosigkeit auf Anteil Schulden und BIP-Wachstum**

	Dependent variable:

	Alo-quote

Anteil der Schulden	0.25^***
	(0.02)

BIP-Wachstum	-0.09^*
	(0.04)

Constant	3.71^***
	(0.24)


Observations	397
R²	0.36
Adjusted R²	0.36
Residual Std. Error	1.89 (df = 394)
F Statistic	110.18^*** (df = 2; 394)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Multiple lineare RegressionArbeitslosigkeit auf Anteil Schulden und BIP-Wachstum
Dependent variable:
Alo-quote
Anteil der Schulden0.25***
(0.02)
BIP-Wachstum-0.09*
(0.04)
Constant3.71***
(0.24)
Observations397
R20.36
Adjusted R20.36
Residual Std. Error1.89 (df = 394)
F Statistic110.18*** (df = 2; 394)
Note:*p<0.1; **p<0.05; ***p<0.01

Varianz wird zum Größten Teil durch die öffentlichen Schulden erklärt
Schätzer für die Verschuldung bleibt in Höhe und Signifikanz bestehen
BIP-Wachstum nur noch auf 10% Niveau signifikant und Koeffizient deutlich kleiner

**Arbeitslosigkeit auf Anteil Schulden und BIP-Wachstum**

	Dependent variable:

	Alo-quote

Anteil der Schulden	0.25^***
	(0.02)

BIP-Wachstum	-0.09^*
	(0.04)

Constant	3.71^***
	(0.24)


Observations	397
R²	0.36
Adjusted R²	0.36
Residual Std. Error	1.89 (df = 394)
F Statistic	110.18^*** (df = 2; 394)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Sample Splits und Interaktionsmodell

Durch die deskriptive Analyse wissen wir, dass es große Unterschiede zwischen ost- und westdeutschen Landkreisen gibt (und das in allen untersuchten Dimensionen).

Gilt der dokumentierte Zusammenhang zwischen dem Anteil der öffentlichen Verschuldung und der Arbeitslosenquote für Ost- und Westdeutschland gleichermaßen?

Sample Splits und Interaktionsmodell

Durch die deskriptive Analyse wissen wir, dass es große Unterschiede zwischen ost- und westdeutschen Landkreisen gibt (und das in allen untersuchten Dimensionen).

Gilt der dokumentierte Zusammenhang zwischen dem Anteil der öffentlichen Verschuldung und der Arbeitslosenquote für Ost- und Westdeutschland gleichermaßen?

Um dieser Frage auf den Grund zu gehen wollen wir im ersten Schritt die Variable Ostdeutschland in unserer Regression hinzufügen:

schulden <- lm(alo_quote ~ anteil_schulden + ost, data=gesamtdaten)
stargazer(schulden,  
          type = "html", header = FALSE, digits = 2,
          title = "Arbeitslosigkeit mit Interaktionstermen",
          dep.var.labels=c("Alo-quote"),
          covariate.labels=c("Anteil Schulden", "Ostdeutschland")
          )

Sample Splits und InteraktionsmodellArbeitslosigkeit mit Interaktionstermen
Dependent variable:
Alo-quote
Anteil Schulden0.22***
(0.02)
Ostdeutschland2.02***
(0.23)
Constant3.20***
(0.15)
Observations397
R20.46
Adjusted R20.46
Residual Std. Error1.73 (df = 394)
F Statistic169.06*** (df = 2; 394)
Note:*p<0.1; **p<0.05; ***p<0.01

**Arbeitslosigkeit mit Interaktionstermen**

	Dependent variable:

	Alo-quote

Anteil Schulden	0.22^***
	(0.02)

Ostdeutschland	2.02^***
	(0.23)

Constant	3.20^***
	(0.15)


Observations	397
R²	0.46
Adjusted R²	0.46
Residual Std. Error	1.73 (df = 394)
F Statistic	169.06^*** (df = 2; 394)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Sample Splits und InteraktionsmodellArbeitslosigkeit mit Interaktionstermen
Dependent variable:
Alo-quote
Anteil Schulden0.22***
(0.02)
Ostdeutschland2.02***
(0.23)
Constant3.20***
(0.15)
Observations397
R20.46
Adjusted R20.46
Residual Std. Error1.73 (df = 394)
F Statistic169.06*** (df = 2; 394)
Note:*p<0.1; **p<0.05; ***p<0.01

Ostdeutschland ist eine Dummyvariable, welche 1 ist für alle ostdeutschen Landkreise
In ostdeutschen Landkreisen ist die Arbeitslosigkeit im Durchschnitt um 2.02 Prozentpunkte höher als in westdeutschen Landkreisen
Koeffizient signifikant auf dem 1%-Signifikanzniveau
Höheres R² (Varianz in der Alo-quote kann besser erklärt werden)
Keine Auswirkung auf den Koeffizienten der öffentlichen Verschuldung

**Arbeitslosigkeit mit Interaktionstermen**

	Dependent variable:

	Alo-quote

Anteil Schulden	0.22^***
	(0.02)

Ostdeutschland	2.02^***
	(0.23)

Constant	3.20^***
	(0.15)


Observations	397
R²	0.46
Adjusted R²	0.46
Residual Std. Error	1.73 (df = 394)
F Statistic	169.06^*** (df = 2; 394)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Sample Splits und Interaktionsmodell

Diese Regression beantwortet jedoch nicht genau unsere Frage!

Wir wollten wissen, ob der Zusammenhang zwischen öffentlicher Verschuldung und Arbeitslosenquote für alle ost- und westdeutschen Landkreise gleichermaßen gilt

Dafür müssen wir die Variable Ostdeutschlandmit der VariablenAnteil Schulden` interagieren!

Sample Splits und Interaktionsmodell

schulden <- lm(alo_quote ~ anteil_schulden + ost, data=gesamtdaten)
ost <- lm(alo_quote ~ anteil_schulden, data=filter(gesamtdaten, ost==1))
west <- lm(alo_quote ~ anteil_schulden, data=filter(gesamtdaten, ost==0))
interaktion <- lm(alo_quote ~ anteil_schulden*ost, data=gesamtdaten)
stargazer(schulden, interaktion, west, ost, 
          type = "html", header = FALSE, digits = 2,
          title = "Arbeitslosigkeit mit Interaktionstermen",
          dep.var.labels=c("Alo-quote"),
          covariate.labels=c("Anteil Schulden", "Ostdeutschland", "Anteil Schulden * Ostdeutschland")
          )

Sample Splits und InteraktionsmodellArbeitslosigkeit mit Interaktionstermen
Dependent variable:
Alo-quote
(1)(2)(3)(4)
Anteil Schulden0.22***0.24***0.24***0.05
(0.02)(0.02)(0.02)(0.07)
Ostdeutschland2.02***3.82***
(0.23)(0.68)
Anteil Schulden * Ostdeutschland-0.18***
(0.07)
Constant3.20***3.12***3.12***6.94***
(0.15)(0.15)(0.15)(0.75)
Observations39739732176
R20.460.470.410.01
Adjusted R20.460.470.41-0.01
Residual Std. Error1.73 (df = 394)1.72 (df = 393)1.66 (df = 319)1.95 (df = 74)
F Statistic169.06*** (df = 2; 394)117.33*** (df = 3; 393)220.33*** (df = 1; 319)0.53 (df = 1; 74)
Note:*p<0.1; **p<0.05; ***p<0.01

**Arbeitslosigkeit mit Interaktionstermen**

	Dependent variable:

	Alo-quote
	(1)	(2)	(3)	(4)

Anteil Schulden	0.22^***	0.24^***	0.24^***	0.05
	(0.02)	(0.02)	(0.02)	(0.07)

Ostdeutschland	2.02^***	3.82^***
	(0.23)	(0.68)

Anteil Schulden * Ostdeutschland		-0.18^***
		(0.07)

Constant	3.20^***	3.12^***	3.12^***	6.94^***
	(0.15)	(0.15)	(0.15)	(0.75)


Observations	397	397	321	76
R²	0.46	0.47	0.41	0.01
Adjusted R²	0.46	0.47	0.41	-0.01
Residual Std. Error	1.73 (df = 394)	1.72 (df = 393)	1.66 (df = 319)	1.95 (df = 74)
F Statistic	169.06^*** (df = 2; 394)	117.33^*** (df = 3; 393)	220.33^*** (df = 1; 319)	0.53 (df = 1; 74)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Sample Splits und Interaktionsmodell

Wie können Sie den Interaktionsterm interpretieren?

Sample Splits und Interaktionsmodell

Wie können Sie den Interaktionsterm interpretieren?

Spalte 2 repräsentiert das Interaktionsmodell
In Spalte 3 und 4 wurden separate Regressionen für alle westdeutschen (Spalte 3) und ostdeutschen (Spalte 4) Landkreise durchgeführt
Analyse von Spalte 2 im Zusammenspiel mit Spalte 3 und 4 erleichtert das Verständis für die Interaktionsvariable

Sample Splits und Interaktionsmodell

Wie können Sie den Interaktionsterm interpretieren?

Spalte 2 repräsentiert das Interaktionsmodell
In Spalte 3 und 4 wurden separate Regressionen für alle westdeutschen (Spalte 3) und ostdeutschen (Spalte 4) Landkreise durchgeführt
Analyse von Spalte 2 im Zusammenspiel mit Spalte 3 und 4 erleichtert das Verständis für die Interaktionsvariable
Konstante:
- In Spalte 3 (für Westdeutsche) bei 3.12, was dem Wert aus Spalte 2 (Interaktionsmodell) entspricht.
- In Spalte 4 (für Ostdeutsche) bei 6.94
- Die durchschnittliche Arbeitslosenquote für einen unverschuldeten ostdeutschen Landkreis liegt deutlich höher als bei einem westdeutschen (3.12 Prozent vs. 6.94 Prozent)

Dieses Ergebnis bekommen wir auch aus dem Interaktionsmodell!

$\to$ Dummy Variable Ostdeutschland und die Konstante aufaddieren: Ostdeutschland + Constant = 3.82 + 3.12 = 6.94!

Sample Splits und Interaktionsmodell

Anteil Schulden:
- In Spalte 3 (für Westdeutsche) bei 0.24, was dem Wert aus Spalte 2 (Interaktionsmodell) entspricht
- In Spalte 4 (für Ostdeutsche) ist der Zusammenhang deutlich kleiner und insignifikant
- Für alle westdeutschen Landkreise gibt es einen signifikanten Zusammenhang zwischen der öffentlichen Verschuldung und der Arbeitslosenquote
- Direkt ersichtlich das der Zusammenhang für ostdeutsche Landkreise signifikant kleiner ist als für westdeutsche (um -0.18 Prozentpunkte, der Koeffizient von Anteil Schulden * Ostdeutschland

$\to$ Wenn wir uns den Zusammenhang für alle ostdeutschen Landkreise berechnen möchten, dann ergibt sich dieser als Anteil Schulden + Anteil Schulden * Ostdeutschland = 0.24 + (-0.18) = 0.06

Die westdeutschen Landkreise dienen uns hier überall als Basislevel!

Sample Splits und Interaktionsmodell

Anteil Schulden:
- In Spalte 3 (für Westdeutsche) bei 0.24, was dem Wert aus Spalte 2 (Interaktionsmodell) entspricht
- In Spalte 4 (für Ostdeutsche) ist der Zusammenhang deutlich kleiner und insignifikant
- Für alle westdeutschen Landkreise gibt es einen signifikanten Zusammenhang zwischen der öffentlichen Verschuldung und der Arbeitslosenquote
- Direkt ersichtlich das der Zusammenhang für ostdeutsche Landkreise signifikant kleiner ist als für westdeutsche (um -0.18 Prozentpunkte, der Koeffizient von Anteil Schulden * Ostdeutschland

$\to$ Wenn wir uns den Zusammenhang für alle ostdeutschen Landkreise berechnen möchten, dann ergibt sich dieser als Anteil Schulden + Anteil Schulden * Ostdeutschland = 0.24 + (-0.18) = 0.06

Die westdeutschen Landkreise dienen uns hier überall als Basislevel!

Vorteil des Interaktionsmodells:

Durch das Interaktionsmodell nutzen wir eine Regression und verwenden den kompletten Datensatz, dadurch hat unsere Regression mehr Power um Effekte zu detektieren.

Sind diese Ergebnisse kausal zu interpretieren?

Basieren auf Beobachtungsdaten
Arbeitslosenquote könnte noch von vielen anderen Faktoren beeinflusst sein, welche wir hier nicht aufgenommen haben (z.B. der Bevölkerungszuwachs oder die Inflation)
Um kausale Effekte messen zu können müssten wir entweder ein kontrolliert randomisiertes Experiment durchführen oder uns ein natürliches Experiment in den Daten zunutze machen

Kausale Antworten auf verschiedenste Fragen wollen wir in den folgenden Vorlesungseinheiten auf der Basis anderer Datensätze tätigen.

Zusammenfassung

Was haben wir über die Arbeitslosenquote in Deutschland gelernt?

Es gibt starke regionale Unterschiede in Deutschland
Der Anteil der öffentlichen Schulden scheint ein wichtiger Faktor zur Vorhersage der Arbeitslosenquote zu sein
Eine fundierte deskriptive Analyse schafft die Grundlage für eine spätere fundierte tiefergehende Analyse mittels linearer Regression

Übungsaufgaben

Im ersten Teil der Case Study hatten Sie sich noch die durchschnittlichen Einkommen auf Landkreisebene in R eingelesen und im zweiten Teil deskriptiv untersucht. Nun sollten Sie diese Tabelle mittels linearer Regression analysieren:

Erstellen Sie eine Regressionstabelle mittels stargazer in der Sie die Arbeitslosenquote auf die Einkommen für das Jahr 2017 regressieren.
- Interpretieren Sie ihre Ergebnisse
Erstellen Sie ein Interaktionsmodell incl. Sample Split mittels stargazer und interpretieren Sie die Ergebnisse ihrer Regressionen.

Organisatorische Hinweise

Bitte bis zum 09.05.2021 angeben ob Sie bei den Projekten in Gruppen zugeteilt werden dürfen

Ohne Zusage keine Gruppe
Ohne Gruppe keine Note

Am 10.05.2021 erfolgt die Zuteilung auf Gruppen und die Tutoriumstermine werden freigegeben

Weitere Daten:

Bis zum 09.05.2021 ist das 5. R-Tutor Problem Set auf Moodle hochzuladen (nur die .sub-Datei!)

Bis zum 16.05.2021 ist das 6. R-Tutor Problem Set auf Moodle hochzuladen (nur die .sub-Datei!)

Ab dem 17.05.2021 steht für Sie wieder eine Probeklausur auf Moodle bereit

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help